Designing experiments is a cornerstone of scientific and industrial progress, from optimizing materials to enhancing processes. Traditional approaches to experimental design have laid the groundwork for discovery, but they come with significant limitations. Enter Gaussian Processes (GP), a machine learning technique that transforms how experiments are planned and executed. In this post, we’ll explore the differences between traditional experimental design methods and the advanced approach implemented in DxTER.

 

Traditional Experimental Design: Tried but Limited

Historically, experimental design has relied on varying one factor at a time to observe how it influences the outcome. While this approach might seem intuitive, it overlooks a critical aspect of experimentation: interactions between factors. A factor’s effect on a response might depend on the levels of other factors, meaning that analysing one variable in isolation can lead to suboptimal conclusions.

To address these limitations, researchers developed more structured experimental design methods:

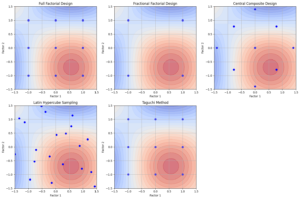
• Full Factorial Design: This approach systematically evaluates all possible combinations of factor levels. It provides a comprehensive understanding of the design space. However, the major drawback is the exponential growth in the number of experiments needed as the number of factors increases, making it highly impractical for designs involving many factors. This quickly becomes resource-intensive and time-consuming.
• Fractional Factorial Design: A more efficient alternative to full factorial designs, fractional factorial designs evaluate only a fraction of the possible combinations of factor levels. While this reduces the number of experiments, the downside is that it sacrifices the ability to detect higher-order interactions. In cases where such interactions are critical, fractional factorial designs can lead to misleading conclusions.
• Central Composite Design (CCD): CCD builds upon factorial designs by introducing additional central and axial points, allowing for the modelling of linear, quadratic, and interaction effects. However, this method can still be expensive in terms of time and resources, as it requires multiple additional points to be tested, especially when dealing with a large number of factors. While more efficient than full factorial designs, it still becomes cumbersome as the number of factors increases.
• Latin Hypercube Sampling: This method divides the range of each factor into intervals and selects points randomly within these intervals. While it ensures a broad exploration of the design space, its limitation lies in its potential for missing critical interactions between factors. If not carefully implemented, Latin Hypercube can provide a skewed representation of the design space, potentially missing key insights.
• Taguchi Method: This method focuses on improving process robustness by using orthogonal arrays to systematically test multiple factors with fewer experiments. It is designed to optimize performance while minimizing variability caused by external factors, often using a signal-to-noise ratio as a key metric. However, the method assumes that the chosen orthogonal array captures all critical interactions, which may not always be the case. Furthermore, its emphasis on robustness can sometimes limit the depth of insights into the underlying system’s behaviour, potentially overlooking subtle or complex relationships between factors.

Even with these advanced methodologies, traditional approaches face significant challenges. As the number of factors grows, the combinatorial complexity of exploring the design space becomes overwhelming. Additionally, balancing multiple objectives, such as optimizing performance while reducing costs, can be difficult to achieve. Furthermore, traditional methods often treat uncertainty as uniform across the design space, which limits their ability to adapt dynamically as new data becomes available.

The AI Advantage: Gaussian Processes (GP)

Modelling the behaviour of responses across unexplored regions of the design space is a challenge that Gaussian Processes (GP) tackle with precision. As a probabilistic technique rooted in machine learning and artificial intelligence, GPs continuously update their predictions using all available data, effectively accounting for uncertainty in a way that traditional methods cannot.

One of the greatest strengths of Gaussian Processes lies in their versatility. Unlike parametric approaches, GPs are non-parametric, meaning they do not require prior assumptions about how factors and responses are related. This makes them ideal for exploring complex systems where the relationships between variables may be unclear or highly nonlinear.

Another defining feature of GPs is their unique ability to manage uncertainty. Instead of assuming that uncertainty is constant across the design space, they adopt a Bayesian perspective. For every prediction, GPs generate a probability distribution for the expected response, which dynamically updates as new data is incorporated. This adaptive approach leads to smarter decision-making and deeper confidence in experimental results.

 

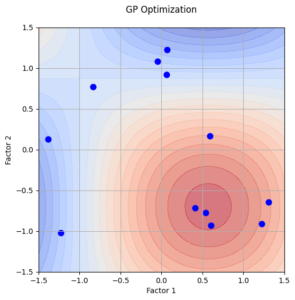
How DxTER Transforms Experimental Design with GP

DxTER leverages the power of Gaussian Processes, a machine learning technique used in artificial intelligence, to optimize experimental workflows, ensuring every experiment is as informative as possible:

• Accelerating the Process: By modelling the design space using GPs, DxTER identifies areas that are most likely to yield valuable insights, significantly reducing the number of experiments needed.
• Reducing the number of Experiments: Instead of testing every possible combination of factors, DxTER uses GP models to predict outcomes and focus on the most promising regions of the design space.
• Resource Optimization: By minimizing the number of experiments required, DxTER saves time, money, and resources, ensuring that experiments are only conducted where they are most needed.

 

The Bottom Line

Traditional experimental design methods have been crucial in advancing science and industry, but they come with inherent limitations, especially as the complexity of the system increases. DxTER’s use of Gaussian Processes, a machine learning technique used in artificial intelligence, offer a more efficient and dynamic way to explore design spaces, accounting for uncertainty and continuously refining predictions. By focusing on the most promising areas and reducing the number of trials, DxTER enables you to reach your experimental goals with fewer resources and less uncertainty. Whether you’re optimizing formulations, processes, or materials, DxTER provides the tools you need to achieve results more efficiently and with greater confidence.